
Table of Contents(目次)
Subsets, Supersets, and Disjoint Sets in Python
In this lecture, we will explain subsets (proper subsets), supersets (proper supersets), and disjoint sets.
These concepts allow us to determine whether one set contains another or whether sets A and B share any common elements.
You do not need to memorize the terms subset, proper subset, superset, proper superset, or disjoint set. In this lecture, the focus is not on terminology but on understanding under what conditions these expressions evaluate to True or False.
How to Use Subset (A<=B) and Proper Subset (A<B) in Python
In mathematics, a set A is a subset of a set B if all elements of A are also elements of B; (...) It is possible for A and B to be equal; if they are unequal, then A is a proper subset of B.
https://en.wikipedia.org/wiki/Subset
In Python, when evaluating a subset (A<=B), the result is True if all elements of set A are contained within set B. This includes the case where "A = B", meaning all elements match exactly.
A proper subset (A < B) is evaluated using the same logic as subset, but when all elements match, it evaluates to False.
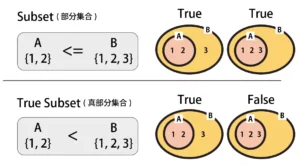
The inequality signs (< / >) used with sets do not represent numeric comparison but indicate whether one set’s elements are contained within another.
For A < B, it returns True if "B contains all elements of A and has additional elements."
For A > B, it returns True if "A contains all elements of B and has additional elements."
Cases where the subset condition evaluates to True include:
B = {1, 2, 3} # Set B is fixed
A = {1, 2, 3} # Subset is True when all elements match
print(A <= B)
A = {1, 2} # The following sets are also True: {2, 3}, {1, 3}
print(A <= B)
A = {1} # The following sets are also True: {2}, {3}
print(A <= B)
A = set() # An empty set for A also results in True
print(A <= B)
Cases where the subset condition evaluates to False include:
B = {1, 2, 3} # Set B is fixed
A = {9} # False if A has elements not in B
print(A <= B)
A = {1, 9} # False if A has elements not in B
print(A <= B)
For proper subsets, the result is False if all elements are the same, but otherwise the results are identical to subsets.
B = {1, 2, 3} # Set B is fixed
A = {1, 2, 3} # Proper subset is False when all elements match
print(A < B) # False
A = {1, 2} # The following sets are also True: {2, 3}, {1, 3}
print(A < B) # True
A = {1} # The following sets are also True: {2}, {3}
print(A < B) # True
A = set() # An empty set for A also results in True
print(A < B) # True
A = {9} # False if A has elements not in B
print(A < B) # False
A = {1, 9} # False if A has elements not in B
print(A < B) # False
How to Use Superset (A>=B) and Proper Superset (A>B) in Python
A superset is essentially the reverse of a subset, with sets A and B swapped. In Python, the inequality signs are reversed accordingly.
In Python, when evaluating a superset (A>=B), the result is True if all elements of set B are contained within set A. This includes the case where "A = B", meaning all elements match exactly.
A proper superset (A > B) is evaluated using the same logic as superset, but when all elements match, it evaluates to False.
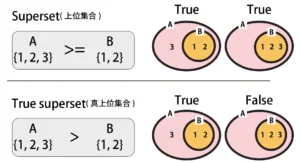
Cases where the superset condition evaluates to True include:
A = {1, 2, 3} # Set A is fixed
B = {1, 2, 3} # Superset is True when all elements match
print(A >= B)
B = {1, 2} # The following sets are also True: {2, 3}, {1, 3}
print(A >= B)
B = {1} # The following sets are also True: {2}, {3}
print(A >= B)
B = set() # An empty set for B also results in True
print(A >= B)
Cases where the superset condition evaluates to False include:
A = {1, 2, 3} # Set A is fixed
B = {9} # False if B has elements not in A
print(A >= B)
B = {1, 9} # False if B has elements not in A
print(A >= B)
For proper supersets, the result is False if all elements are the same, but otherwise the results are identical to supersets.
A = {1, 2, 3} # Set A is fixed
B = {1, 2, 3} # Proper superset is False when all elements match
print(A > B) # False
B = {1, 2} # The following sets are also True: {2, 3}, {1, 3}
print(A > B) # True
B = {1} # The following sets are also True: {2}, {3}
print(A > B) # True
B = set() # An empty set for B also results in True
print(A > B) # True
B = {9} # False if B has elements not in A
print(A > B) # False
B = {1, 9} # False if B has elements not in A
print(A > B) # False
Checking Disjoint Sets with isdisjoint() in Python
Disjoint sets are sets that share no common elements.
In Python, there is no operator for disjoint sets, so the isdisjoint() method is used instead.
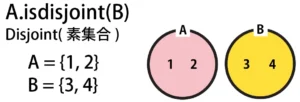
A = {1, 2}
B = {3, 4}
result = A.isdisjoint(B)
print("Disjoint:", result) # True
If even a single common element exists, the result is False.
A = {1, 2, 3}
B = {3, 4}
result = A.isdisjoint(B)
print("Disjoint:", result) # False






