
Table of Contents(目次)
Pythonの集合演算に使うサンプルデータについて
このレクチャーでは集合演算を学習します。
各演算で使用するデータは、次の2種類のsetです。
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
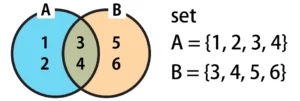
変数"A"は1~4の数値のデータを持っており、ベン図で表すと、青枠の範囲のデータを持っています。
変数"B"は3~6の数値のデータを持っており、ベン図で表すと、オレンジ枠の範囲のデータを持っています。
そして、変数"A","B"は、{3, 4}を共通の値として持っています。(ベン図の、丸枠が重なっている部分。)
Pythonのsetで和集合(union)を求める方法: 演算子 |
和集合は、AとBが所持している値の範囲を合わせた結果を返します。ベン図で示すと、下図の緑枠の範囲になります。
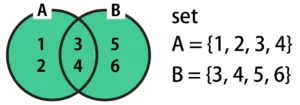
Pythonで和集合を取得したい場合は、次のコードのように、AとBの間に|(バーティカルライン)を挟みます。
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
union = A | B
print("union:", union) # {1, 2, 3, 4, 5, 6}
A | Bと記述すると、和集合のsetが新たに生成され、変数"union"へ代入されます。結果は、{1, 2, 3, 4, 5, 6}となります。 (AとBの演算が行われ、新しいsetが生成されるという挙動は、積集合・差集合・対称差でも同じです。)
なお、変数"A","B"の共通の値である{3, 4}は、重複が取り除かれます。
Pythonのsetで積集合(intersection)を求める方法: 演算子 &
積集合は、AとBが所持している値の重なっている範囲を結果として返します。ベン図で示すと、下図の緑枠の範囲になります。
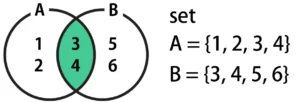
Pythonで積集合を取得したい場合は、次のコードのように、AとBの間に&を挟みます。
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
intersection = A & B
print("intersection:", intersection) # {3, 4}
Pythonのsetで差集合(difference)を求める方法: 演算子 -
差集合は、ある集合から、他方の集合の範囲を差し引いた範囲を結果として返します。
差集合は-演算子で表します。
集合AとBがあったとき、A - BとB - Aの結果は異なります。
Pythonの差集合 A - B の例
A - Bの差集合は、AからBを差し引いた範囲を結果として返します。ベン図で示すと、下図の緑枠の範囲になります。Bの範囲(図のグレーの部分)の値が取り除かれることになるので、Aから{3, 4}が取り除かれた、{1, 2}が結果として返ります。
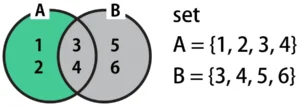
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
difference_AB = A - B
print("difference_AB:", difference_AB) # {1, 2}
Pythonの差集合 B - A の例
B - Aの差集合は、BからAを差し引いた範囲を結果として返します。ベン図で示すと、下図の緑枠の範囲になります。Aの範囲(図のグレーの部分)の値が取り除かれることになるので、Bから{3, 4}が取り除かれた、{5, 6}が結果として返ります。
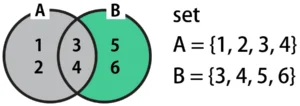
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
difference_BA = B - A
print("difference_BA:", difference_BA) # {5, 6}
Pythonのsetで対称差(symmetric_difference)を求める方法: 演算子 ^
対称差は、AとBが重ならない範囲を結果として返します。ベン図で示すと、下図の緑枠の範囲になります。
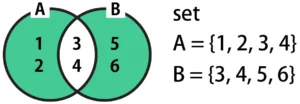
Pythonで対称差を取得したい場合は、次のコードのように、AとBの間に^(キャレット )を挟みます。
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
symmetric_diff = A ^ B
print("symmetric_diff:", symmetric_diff) # {1, 2, 5, 6}






